In computer science, it is very important that we have a way of measuring the efficiency of an algorithm. There are two forms of this efficiency – time complexity (worst case running time) and space complexity (worst case amount of space needed at any point).

The running time of an algorithm depends on many factors other than the efficiency of the algorithm itself: the speed of the programming language computer, the compiler implementation, the available system resources, etc..

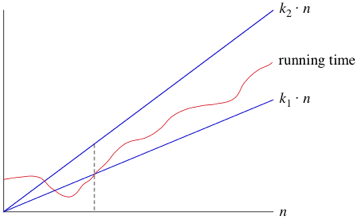
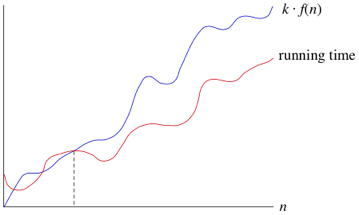
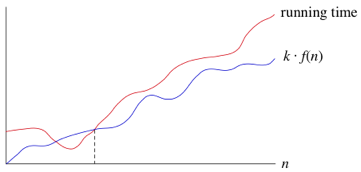
So, our system should be relatively consistent across all these factors, while still delivering valuable information about how long an algorithm takes, and how fast it grows with the input size.

To keep things manageable, we need to simplify the function to distill the most important part and cast aside the less important parts. For example, suppose that an algorithm, running on an input of size n, takes $$ f(n) = 8n^2 + 20n + 20 $$ time. The 8n^2 term grows at a far greater rate than the lower degree terms, as seen below:

⊕ The red function is $$ 8n^2 $$; the purple function is $$ 20x + 20 $$

Thus, we can drop the less significant terms because they have only a small impact on the time complexity, and the constant coefficients because they are dependent on extraneous variables (e.g., computer speed). This new function, simply $$ 8n^2 $$, is written in what we call asymptotic notation. We’ll see three forms of it: big-Θ notation, big-O notation, and big-Ω notation.

⊕ We use big-Θ notation to asymptotically bound the growth of a running time to within constant factors above and below.

⊕ We use big-O notation for asymptotic upper bounds, since it bounds the growth of the running time from above for large enough input sizes. For the previous example, it would be $$ O(n^2) $$

⊕ We use big-Ω notation for asymptotic lower bounds, since it bounds the growth of the running time from below for large enough input sizes.